{ J. Einasto, Mitteilungen der Astronomischen Gesellschaft, Vol. 77, p.19, 1994 }

In October 22, 1993 astronomical world celebrated the Centenary of Professor Dr Ernst Öpik, one of the most outstanding astronomers of the 20th century. Born in a small town Kunda in Estonia he studied privately mathematics, physics and astronomy in high school. When he entered Moscow University he already had a wide knowledge in all these fields and was able to start astronomical research during his student years. After he finished the University courses he was left in Moscow University to prepare for the professorship. In turbulent years of the revolution the University was evacuated to Tashkent, and here Öpik continued his astronomical studies until 1921 when it was possible for him to return to his native Estonia. Here he became the astronomer of the Tartu University Observatory, a post with some teaching obligations but a complete freedom to study. From Tartu he made long scientific visits to other observatories, in particular to the Harvard University Observatory. By the end of World War II, before Soviet Army again occupied Estonia in 1944 he was able with his family to evacuate to Germany. Here he became the Estonian Rector of the Baltic University, formed to help young refugees from three Baltic countries to get the university education. The University stopped his activity after some years, and in 1948 Öpik got a permanent position at Armagh Observatory in Northern Ireland. Some years later he got a position also at Maryland University, and spent his time alternately in Armagh and Maryland. He continued his active scientific life until his 90s, i. e. over 70 years. He died on September 10 1985.

Ernst Öpik has made pioneering contributions in almost all fields of astronomy. The most striking feature in his contributions is freshness of ideas, and the skill to make correct deductions at a time when observational and theoretical evidence favoring one or another point of view was still rather controversial. We consider here as examples some of his contributions to cosmology and related fields which have widened our horizon in understanding the world around us.

The main goal of astronomical studies, in particular of cosmology, is to understand our position in the Universe, the formation and evolution of the Universe and its principal constituents - planets, stars, and stellar systems. Ancient astronomers accepted the view taken from myths of different nations, that the Earth lies in the centre of the World, and the Sun and planets circle around the Earth in orbits of different radii and form. The first flaw to this ancient picture was thrown by Copernicus who demonstrated that the Sun, not the Earth must be placed in the centre of the World. This change of views was so important (since it contradicts the cosmological concept formulated in the Bible) that it marks the formation of the whole modern science.

The next important step in widening our cosmological horizon was taken in the middle of the 19th century, when 3 astronomers almost simultaneously demonstrated that the Sun is also not in the centre of the World, but is an ordinary star among millions of other suns. This step was done by W. Bessel in Königsberg, by F.G.W. Struve in Tartu (Dorpat), and by W. Henderson in Cape-Town, by measuring distances of stars.

The next big step in cosmology was made in the 20s of this century. At this time most astronomers believed that our Milky Way system of stars is the principal constituent of the Universe. Remember that Sir Arthur Eddington (1914) wrote his famous book "Stellar Movements and the Structure of the Universe" where he considered the Milky Way as the principal constituent of the Universe. A hot topic was the discussion on the nature of spiral nebulae -are they gaseous objects within the Milky Way system or distant worlds similar in structure to our Galaxy? Arguments in favor of both concepts were serious and it was difficult to decide who has right.

This problem interested also E. Öpik. In 1918 he delivered a talk in the Meeting of the Moscow Society of Amateur Astronomers, devoted to his study of the structure of the Andromeda Nebulae, M31. The paper was published a few years later (Öpik 1921). Just recently first relative velocity measurements of objects in M31 were published, and Öpik quickly developed a method how to estimate distances to spiral nebulae from relative velocities within them. He used the Newton law

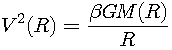
where V(R) is the relative velocity of a test particle at a distance R from the centre of the system (in respect to the mean velocity of the system), G is the constant of gravity, is a constant which depends on the shape and structure of the system (on the fraction of the observed velocity in respect to the velocity of a body moving around the centre of the system in a circular orbit), and M(R) is the mass of the system within a sphere of radius R.

The mass can be substituted with luminosity and mass-to-luminosity ratio, the apparent luminosity of the central part of M31 can be derived from photometric observations, this is to be compared with the absolute luminosity of the Sun to get the mass and luminosity in solar units. Apparent luminosity decreases with increasing distance proportional to the square of the distance, R in the above formula can also be expressed through apparent distance within M31, and the distance of M31 from us. Finally Öpik gets a formula which expresses the distance to M31 through the apparent magnitude of the central part of M31, the mass-to-luminosity ratio in this region, and the respective relative velocity. To estimate the parameter he developed a model of M31. This is actually the first mass distribution model of a galaxy.

His result of the distance depends, of course, on the mass-to-luminosity ratio adopted for M31. Initially he accepted for this quantity a value 1.54 in solar units, based on measurements of the stellar luminosity function in the Solar neighbourhood (Kapteyn 1904), and Öpik's (1915) own estimates of the mass density of the matter in the solar neighbourhood. From these data he gets for the distance 785 kiloparsecs (kpc). A few years later he made a new estimate (Öpik 1922a) using new determinations of the luminosity function by Kapteyn and van Rhijn (1920), and data by Jeans (1922) on the mass density in the solar neighbourhood. His new value for the mass-to-luminosity ratio is 2.63 in solar units which gives for the distance of the Andromeda nebula 440 kpc.

A few years later Hubble (1925a) determined the distance to NGC6822, a member of the Local Group of galaxies, from the apparent brightness of cepheids with the result 214 kpc. Using a similar method Hubble (1929a) found for the distance of M31 275 kpc. The modern value of the distance is 690 kpc.

Öpik (1922a) stresses that his result is completely independent on the assumption on the physical nature of objects in M31 (gas or stars), an important argument in the discussion on the nature of spiral nebulae. At this time the dynamical distance determination method suggested by Öpik was not taken very seriously, and the astronomical community accepted generally the extragalactic nature of spiral nabulae only after Hubble has detected cepheids in M31 and other members of the Local Group and determined the photometric distance. His value is much less than the presently accepted distance. This shows that Öpik's dynamical method was more reliable. A modern version of this method was developed by Fisher and Tully and is widely used in extragalactic astronomy today.

In first decades of this century most astronomers accepted the view that the whole stellar Universe is very old, of the order of 1014 years. This age estimate is based on the observation that stellar orbits in our Milky Way system are well mixed and relaxed. The relaxation time of this process by star-star encounters is very long, of the order mentioned above, and this estimate was taken as the possible age of the Universe. Öpik soon realized that this estimate is not correct, and that the Universe is much younger.

In the 20s radial velocities of some tens of galaxies were measured, and almost all of them showed a shift of spectral lines to the red part of the spectrum - i. e. lines were redshifted. The shift is the larger the fainter galaxies are, and soon the hypothesis was made that the whole Universe is expanding, the expansion velocity being proportional to the distance of the galaxy (Hubble 1929b). The constant of proportionality of this law is now called the Hubble constant, and is one of the principal constants not only in astronomy but in physics in general. The reciprocal value of this constant has a dimension of time, and measures the time from the beginning of the expansion for constant expansion speed.

Öpik (1933) was the first to realize that this time (called the Hubble time in modern cosmology) is approximately equal to several other completely independent fundamental age estimates. He finds an age ~2xlO9 years, and writes: "if we regard the observed motion of the spirals as real, and trace the changes observed at present backwards, we find that a few thousand million years the universe was in a peculiar, more concentrated state, from which it started expanding, possibly as a result of some cataclysm".

The second independent age estimate is the age of the Earths as derived from the decay of heavy radioactive elements, up to 5 billion years. Meteorites also have an age of the same order.

The third age estimate comes from Öpik's studies of double stars and related questions of stellar structure.

At this time astronomers adopted the Russel hypothesis on stellar evolution: stars born as red giants, contract to form blue giants, and then cool and move along the dwarf branch (main sequence) towards red dwarfs. It is well known that the mean mass of stars in the main sequence is not constant - O and A type stars have masses 10-30 Solar masses, whereas masses of red dwarfs are only a fraction of the Solar mass. Öpik (1922b) concludes that, if the Russel hypothesis is correct, the star evolution should be accompanied with mass loss. If mass loss occurs in double stars, the distance between components must increase from blue to red stars of the main sequence, the expected increase is approximately 20 times. To check this result Öpik (1923) studied double stars, and found, that contrary to the expectation, the mean distance between components of red dwarf double stars is about 2 times less than the mean distance of giant doubles.

Öpik gives a second fact contra Russel hypothesis which comes from geological data. The mean temperature on the Earth surface has been almost constant during the whole geological history. If the Sun evolves according to Russel hypothesis its luminosity must decrease along the main sequence by a factor of thousand, and it is impossible to avoid similar changes of the temperature on the Earth.

These results demonstrate that the Hertzsprung-Russel diagram is not an evolutionary diagram but a diagram of various initial conditions - mass, and composition. The energy production per unit mass of blue giants is much higher than that of red dwarfs, thus the energy production must depend on physical conditions in the star. In faint companions of double stars (i. e. on main sequence stars) the luminosity per unit mass is proportional to the mass in 9th power (Öpik 1923). The basic physical parameter which changes among main sequence stars of different mass is the temperature, thus a similar dependence must be valid also for the temperature. Since the temperature rises inward, the energy source of stars must be located near the centre (Öpik 1922b).

Energy sources considered earlier (cooling and radioactive decay) are not temperature dependent, thus Öpik (1922b) realized that the source of stellar energy must be of some "subatomic" nature. The progress in physics was sufficient for Öpik to declare in 1933 that the main source of energy in stars is the burning of hydrogen to helium. The energy output of stars is well known, and Öpik used the energy production rate in the hydrogen burning reaction to calculate ages of stars. For massive O and A type stars of the main sequence he got ages of several tens of millions of years and concluded that, in order to have such stars in the Galaxy, the star forming process must occur in the Galaxy in the present epoch. For stars similar to the Sun Öpik got ages of the order of several billion years, i. e. ages close to the age of the Earth.

Summarizing the results of these completely independent age estimates Öpik (1933) writes: "we may say that the combined evidence presented by meteorites, by statistical data relating to wide double stars, by the distribution of stellar luminosities in globular clusters, and by the observed recession of spiral nebulae, all this evidence points to an age of the stellar universe of the same order of magnitude as the currently accepted age of the solar system: not much more than 3000 million years".

Modern data yield for all three ages larger values, from 10 to 20 billion years. But the method is the same as suggested by Öpik in the early 30s.

With these discoveries Öpik created modern yardsticks of distances and ages of the Universe around us. Remembering these discoveries today it is useful to observe how Öpik was able to find the correct answer to problems in spite of controversial data and widely different opinions of authorities. He often calls his approach to solve new problems as a morphological one. In this notion he emphasizes that in studying new phenomena it is important to take into account all the complexity of problems. In the Introduction of his major paper on the stellar structure and evolution Öpik (1938) explains his approach to study new phenomena as follows: "stellar structure is a physical, not a mathematical problem. What matters are the premises, not the exact mathematical deductions from given premises; we want to know the actual physical conditions determining stellar structure and evolution; a correct mathematical theory may then easily follow. We believe that a mere qualitative picture, taking into account all the complexity of the conditions in stellar interiors, is still a better approximation to the truth than an exact mathematical theory based on simplifications which do not take into account certain most important factors of stellar structure and evolution".

References

Eddington, A.S., 1914, Stellar Movement and the Structure of the Universe, McMillan and Co., London.

Hubble, E., 1925, Astrophys. /., 62, 409.

Hubble, E., 1929a, Astrophys. J., 69, 103.

Hubble, E., 1929b, Proc. Nat. Acad. Sci. 15, 168.

Jeans, J.H., 1922, Mon. Not. R. astr: Soc. 82, 130.

Kapteyn, J.C., 1904, Astron. J. 24, 115.

Kapteyn, J.C. and van Rhijn, P., 1920, Astrophys. J. 52, 23.

Öpik, E., 1915, Bull, de la Soc. Astr. de Russie, 21, 150.

Öpik, E.,  1921, Mirovedenie, 10, 12.

Öpik, E.,  1922a, Astrophys. J., 55, 406.

Öpik, E., 1922b, Publ. Tartu Astr. Obs., 25, No. 2.

Öpik, E.,  1923, Publ. Tartu Astr. Obs., 25, No. 5.

Öpik, E.,  1933, Popular Astronomy, 41, 71.

Öpik, E.,  1938, Publ. Tartu Astr. Obs., 33, No. 3.